Дроби. Действия с дробями

Какими бывают дроби?

а) обыкновенные:

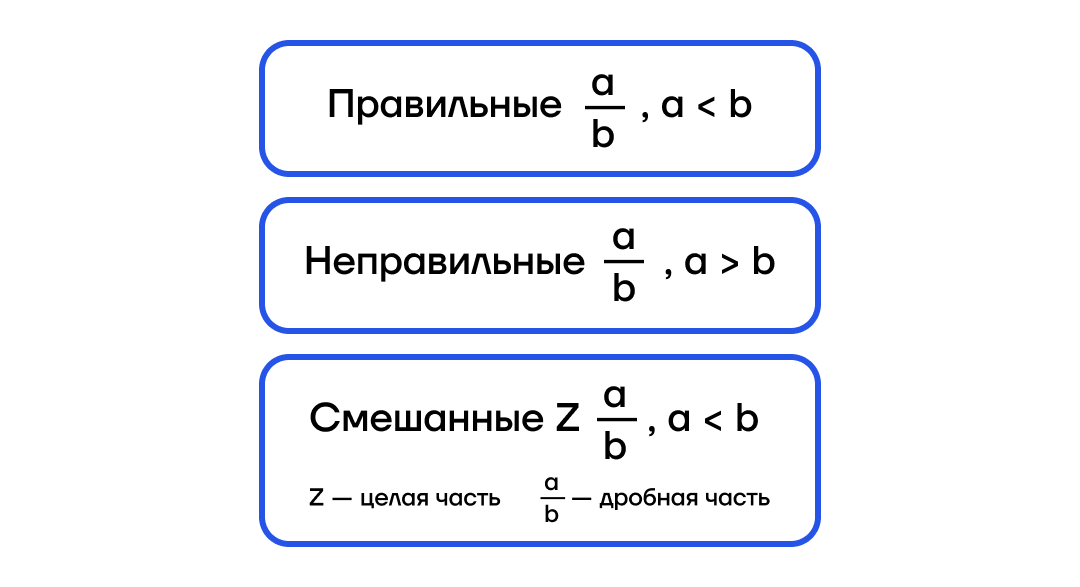
б) десятичные:

• конечные (например: 0,6; 0,8; 1,35);

• бесконечные (например: 1,24768...).

Основное свойство дроби

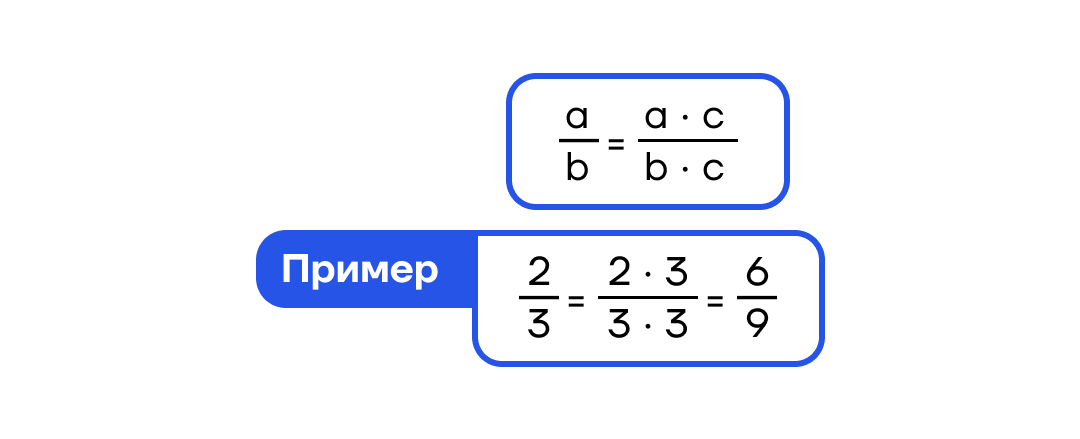
Умножаем числитель и знаменатель на одно и то же число => значение дроби не меняется.

Сокращение дробей

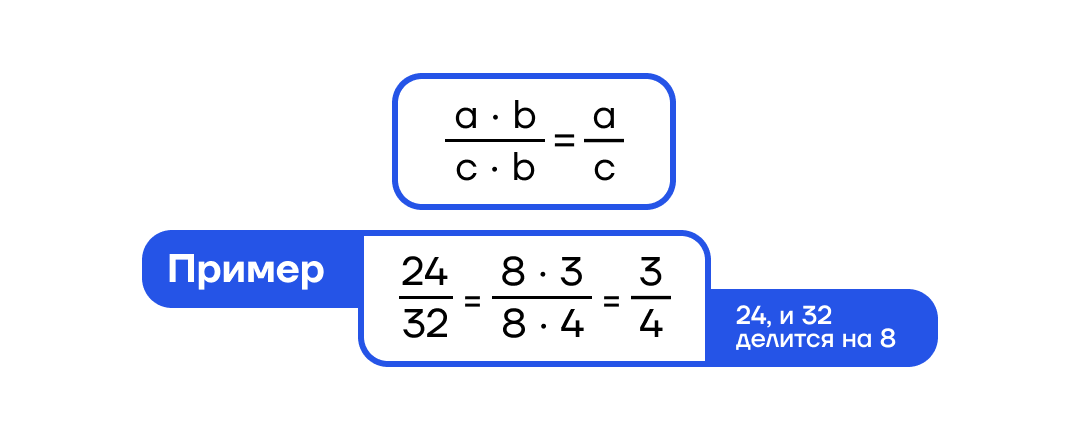
Если мы видим, что и числитель, и знаменатель делятся на какое-то одинаковое число, мы делим (и числитель, и знаменатель) на это число => сокращаем.

Перевод смешанного числа в неправильную дробь

Перевод из неправильной дроби в смешанную

Действия с обыкновенными дробями

Сложение обыкновенных дробей

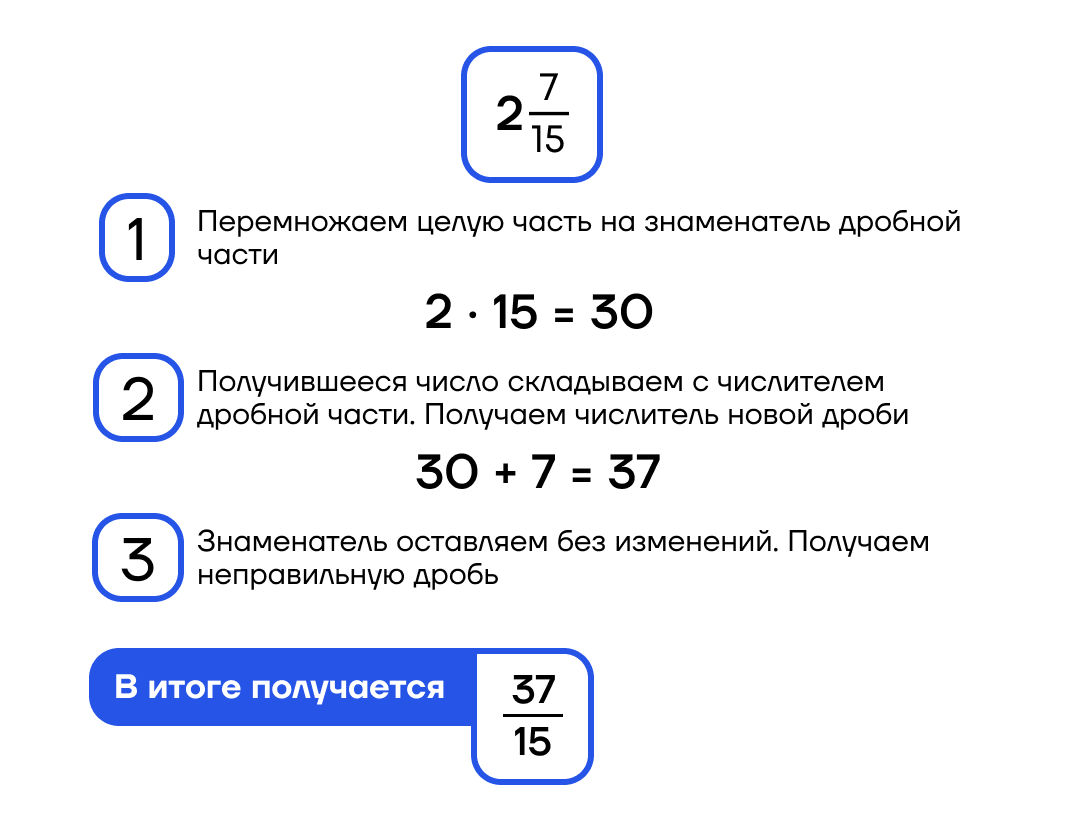
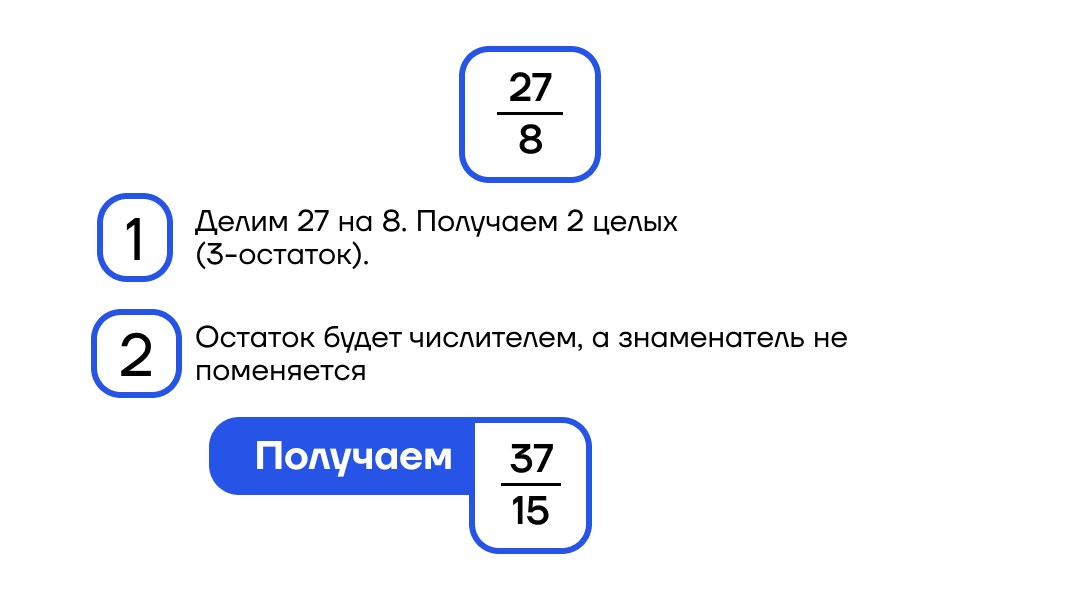
Сложение дробей с одинаковыми знаменателями:

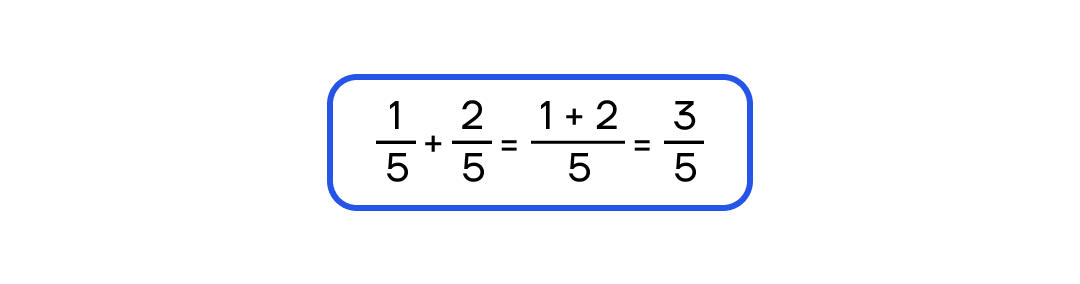
Складываем числители, а знаменатель оставляем без изменения.

Сложение дробей с разными знаменателями:

 

• Привести дроби к наименьшему общему знаменателю.
• Сложить числители дробей, а знаменатель оставить без изменений.

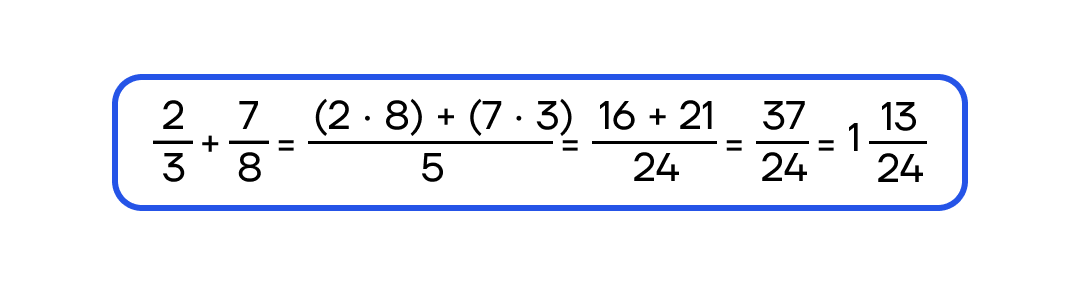
Наименьший общий знаменатель - наименьшее число, которое делится на все знаменатели выражения.

(Можно найти общий знаменатель, необязательно наименьший. Общий знаменатель - число, которое делится на все знаменатели выражения).

Вычитание обыкновенных дробей

Вычитание дробей с одинаковыми знаменателями

 

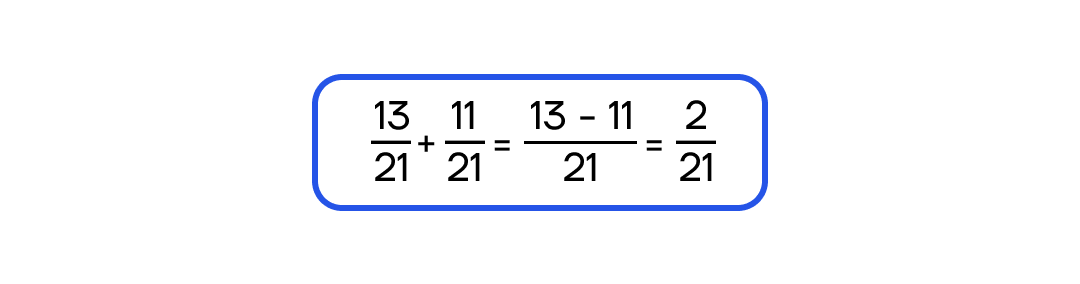
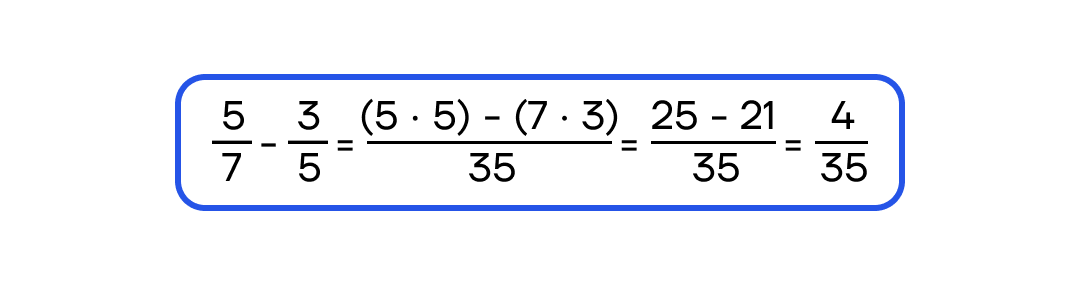
Вычитаем из первого числителя второй, знаменатель оставляем без изменения.

Вычитание дробей с разными знаменателями

 

• Привести дроби к наименьшему общему знаменателю, умножить числители на дополнительные множители.
• Из числителя первой дроби вычесть числитель второй дроби, а знаменатель оставить без изменений.

Умножение обыкновенных дробей

Чтобы умножить две обыкновенные дроби, надо перемножить числители и знаменатели дробей.

Деление обыкновенных дробей

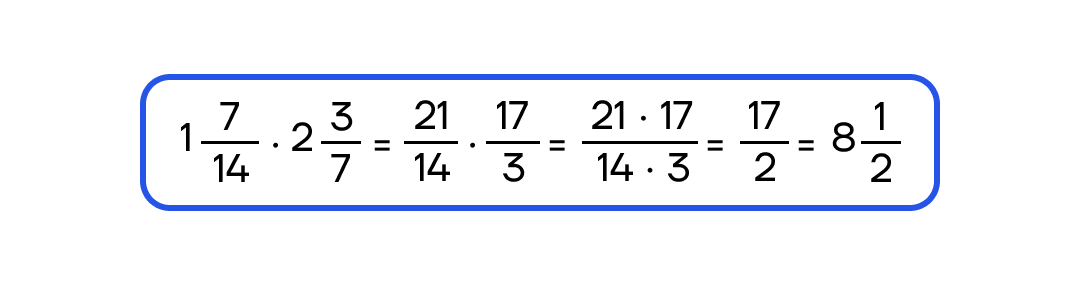
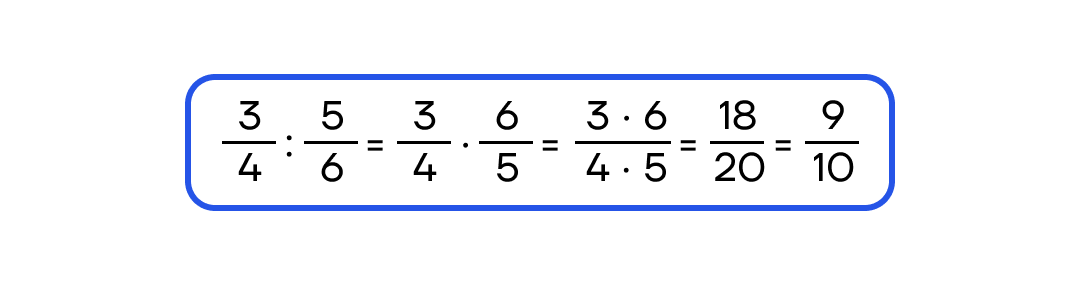
Чтобы разделить одну обыкновенную дробь на другую, надо умножить первую дробь на «перевернутую» вторую.

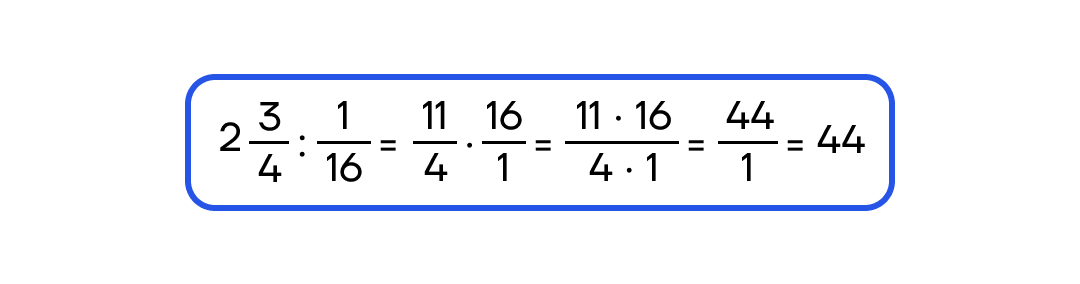
Чтобы разделить одно смешанное число на другое, надо преобразовать смешанные дроби в неправильные, а потом проделать действие деления, как в предыдущем пункте.

Действия с десятичными дробями

Сложение и вычитание десятичных дробей

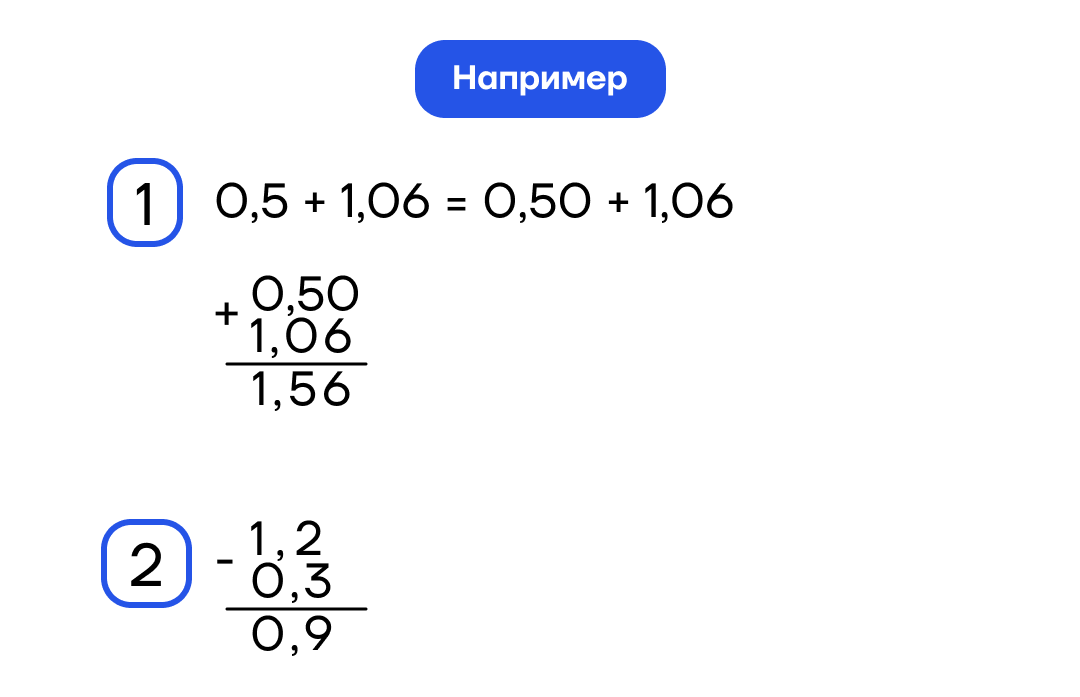
Чтобы сложить (вычесть) десятичные дроби, нужно:

• Уравнять в этих дробях количество знаков после запятой.
• Записать их друг под другом так, чтобы запятая была записана под запятой.
• И просто сложить или вычесть, не теряя запятую.

Умножение десятичных дробей

Чтобы перемножить две десятичные дроби, нужно их перемножить, не обращая внимания на запятые, затем в ответе отделить запятой столько цифр, сколько их было у обоих чисел вместе.

Например:

0,2∙0,03=0,006.

Мы видим, что у первой дроби один знак после запятой, у второй дроби два знака после запятой, значит, в ответе будет 3 (1+2) знака после запятой.

Деление десятичных дробей

Чтобы разделить число на десятичную дробь нужно:

• Умножаем делимое и делитель на 10, 100 и т.д. — так, чтобы делитель превратился в натуральное число.
• Делим натуральные числа.

Например:

4,82:0,2=482:20=24,1(в данном случае мы домножили дробь на 100).