Треугольники

Основное

1. Сумма всех углов треугольника равна 180°.

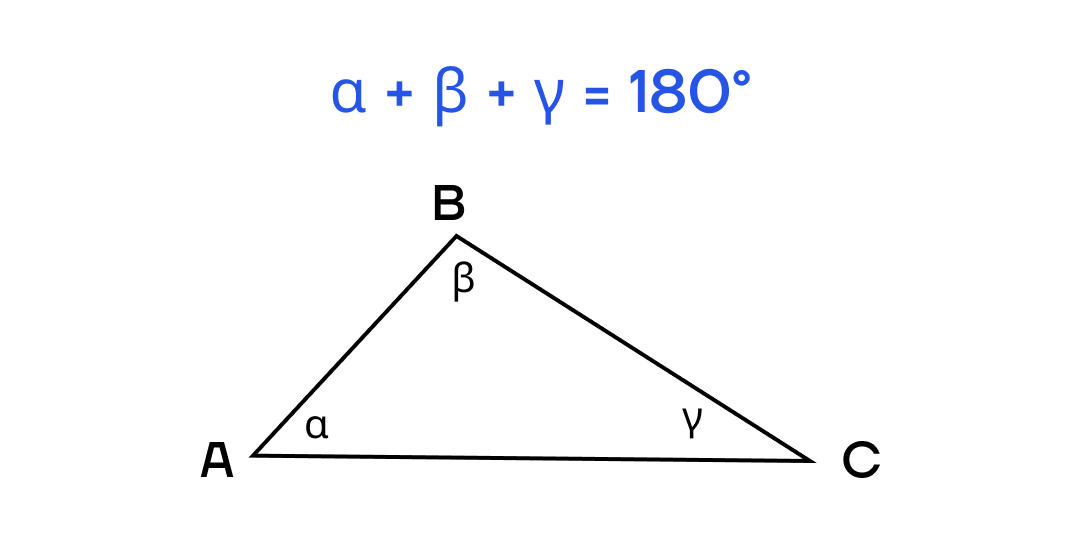
2. Биссектриса любого угла треугольника делит этот угол пополам.

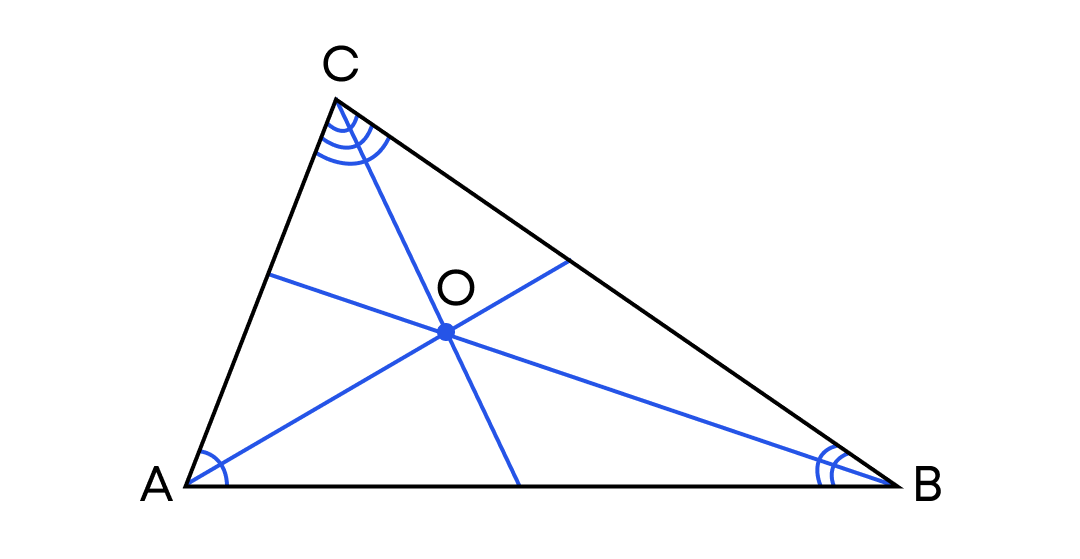
Биссектрисы всех углов треугольника пересекаются в одной точке.

2.1. Точка пересечения биссектрис треугольника является центром вписанной в треугольник окружности.

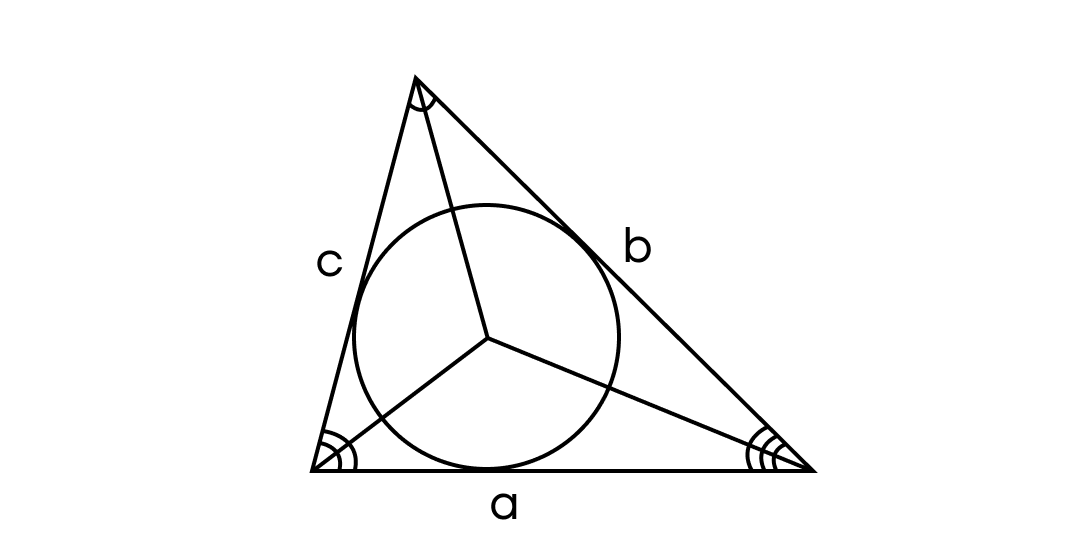
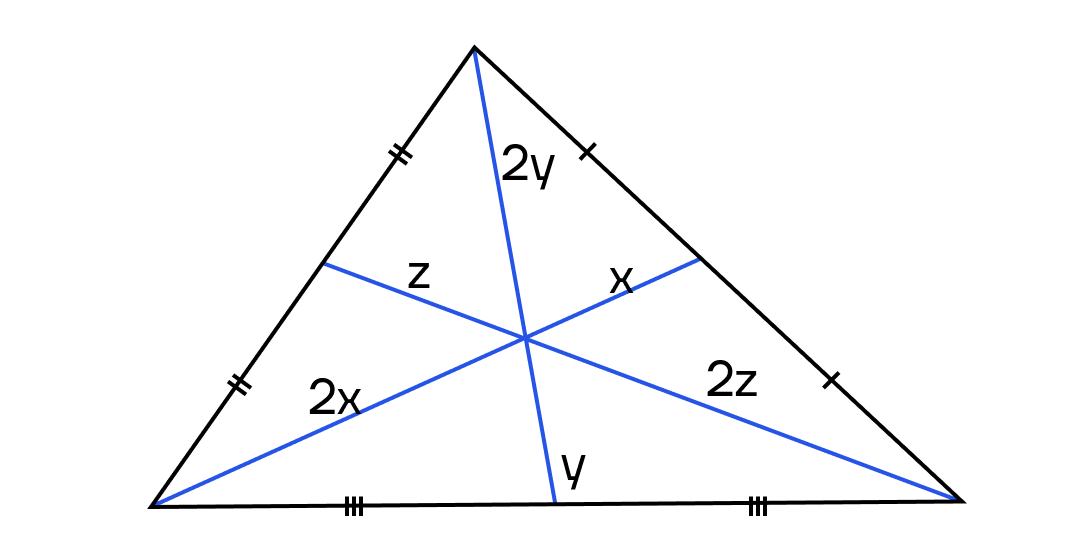
3. Медиана делит сторону, к которой она проведена, на две равные части.

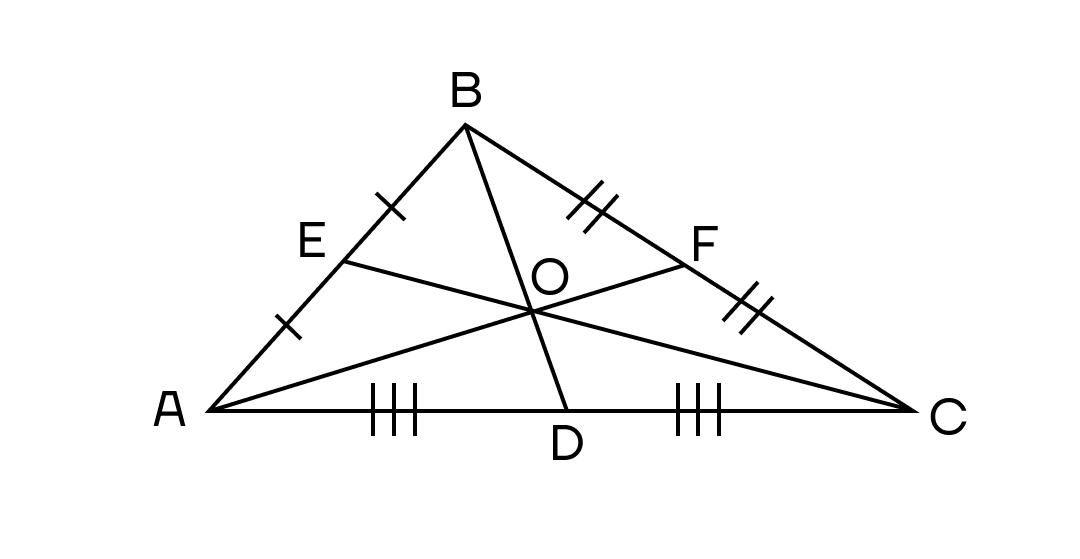
Все три медианы треугольника пересекаются в одной точке.

3.1. Все три медианы треугольника пересекаются в одной точке, которая называется центроидом или центром тяжести треугольника, и делятся этой точкой на две части в отношении 2:1, считая от вершины.

4. Высота — это перпендикуляр к проведенной стороне.

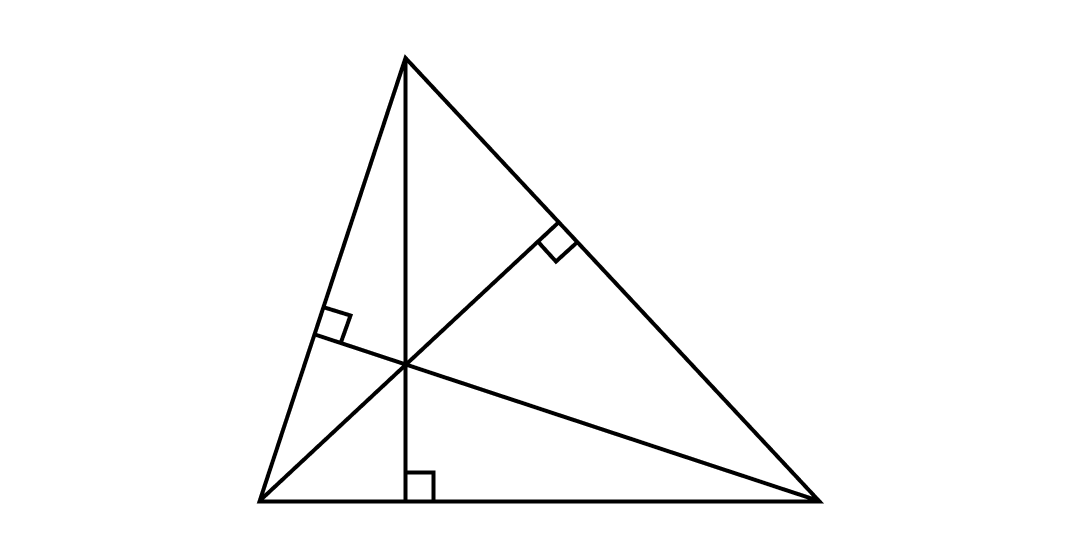
Все высоты треугольника пересекаются в одной точке.

5. Средняя линия треугольника — отрезок, соединяющий середины двух сторон треугольника.

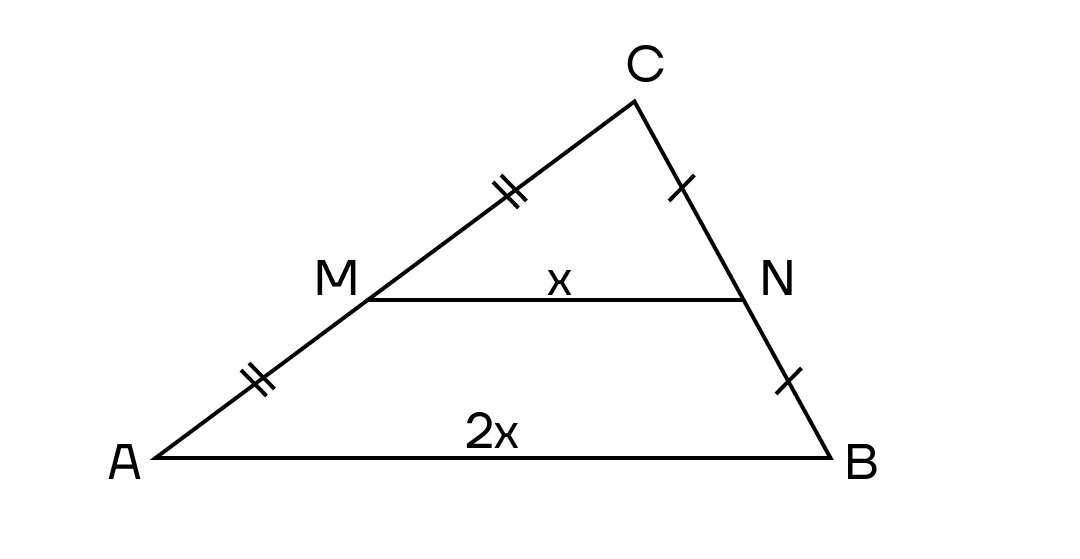
5.1. Средняя линия треугольника параллельна третьей стороне, а ее длина равна половине длины этой стороны.

5.2. Признак средней линии треугольника: если отрезок в треугольнике проходит через середину одной из его сторон, пересекает вторую и параллелен третьей — этот отрезок можно назвать средней линией этого треугольника.

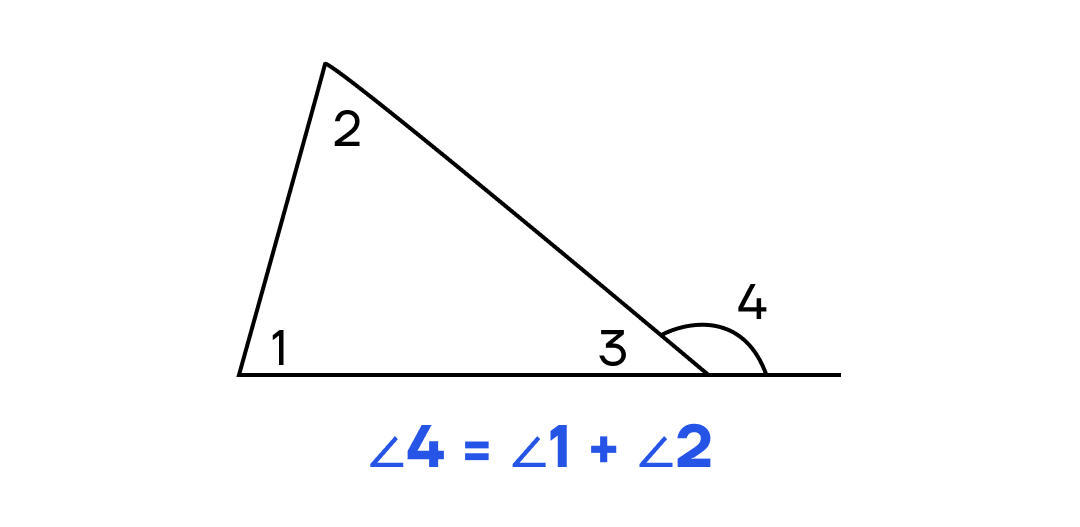
6. Внешний угол треугольника равен сумме двух оставшихся углов треугольника, не смежных с этим внешним углом.

Равнобедренный треугольник

1. Боковые стороны равнобедренного треугольника равны.
2. Углы при основании равны.
3. Медиана, биссектриса и высота, проведенные к основанию, в равнобедренном треугольнике совпадают и делят треугольник на два равных прямоугольных треугольника.

Равносторонний треугольник (правильный)

1. Все стороны равностороннего треугольника равны.
2. Все углы равностороннего треугольника равны.

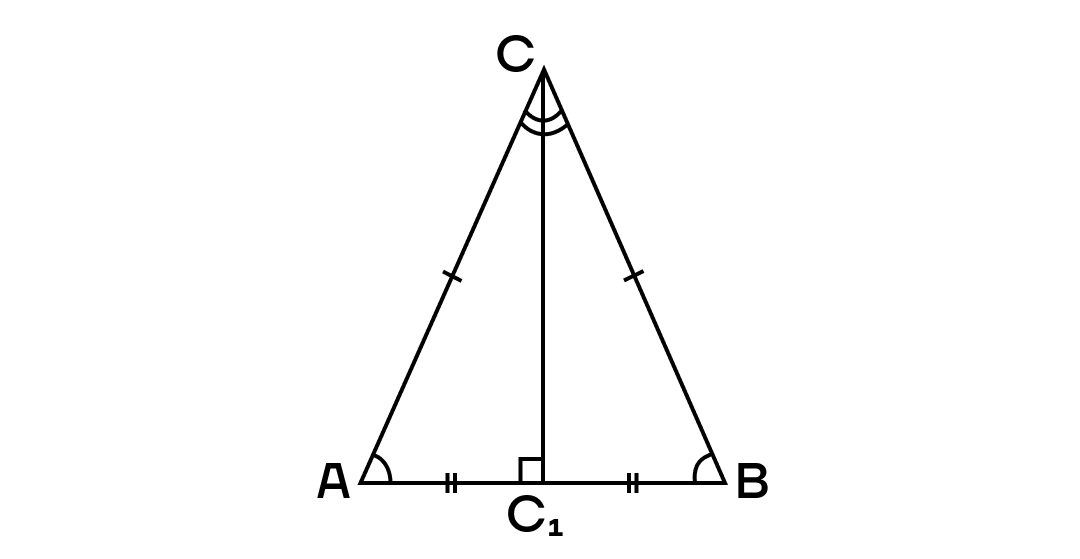
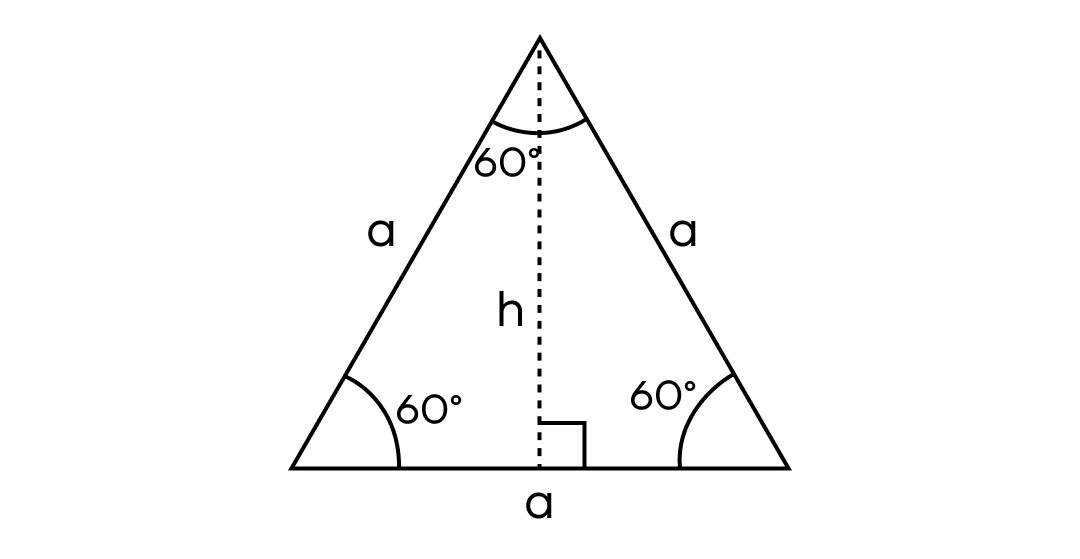
180°:3=60° — каждый угол правильного треугольника.

3. «Как ни крути» равносторонний треугольник будет всегда одновременно и равнобедренным. А, значит, правильный треугольник имеет все свойства равнобедренного.

Получается: медиана, высота, биссектриса, проведенные из одного угла в правильном треугольнике будут совпадать.

Теорема синусов

Таблица синусов и косинусов

Теорема косинусов

Все необходимые формулы площади треугольника

Прямоугольный треугольник

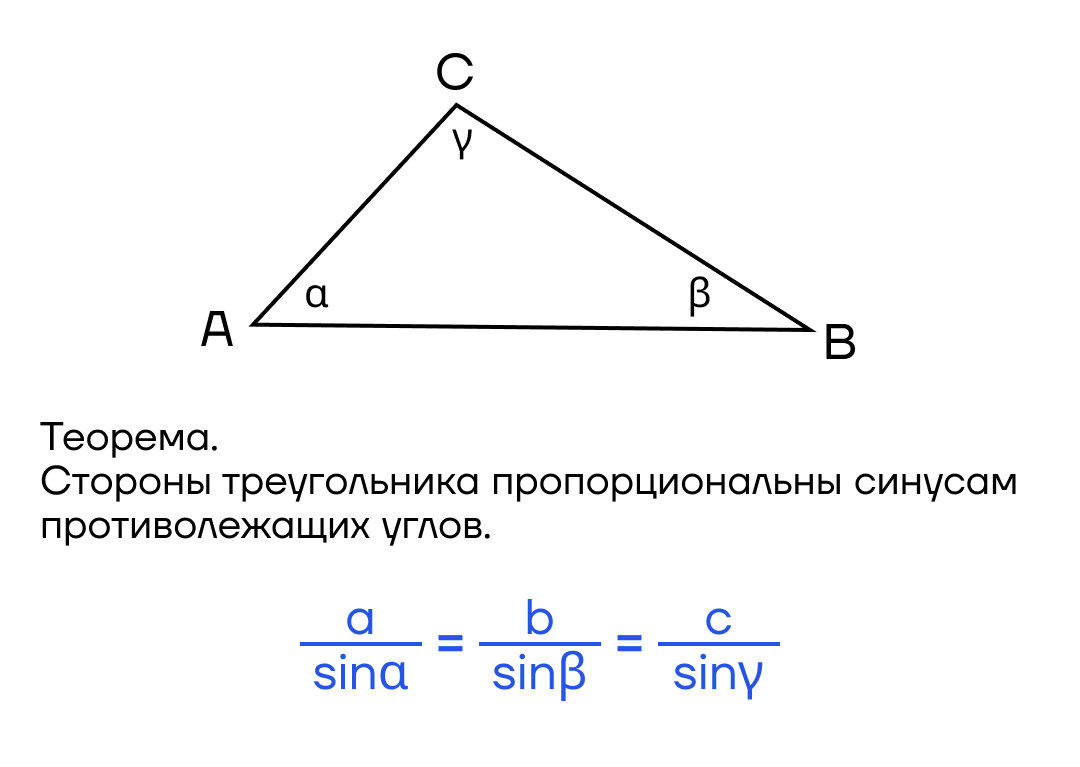
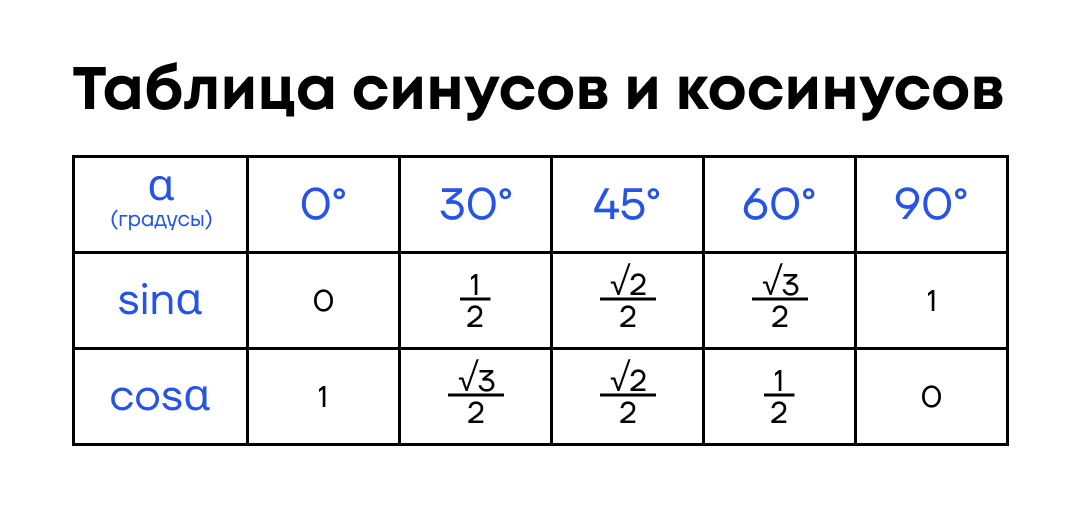
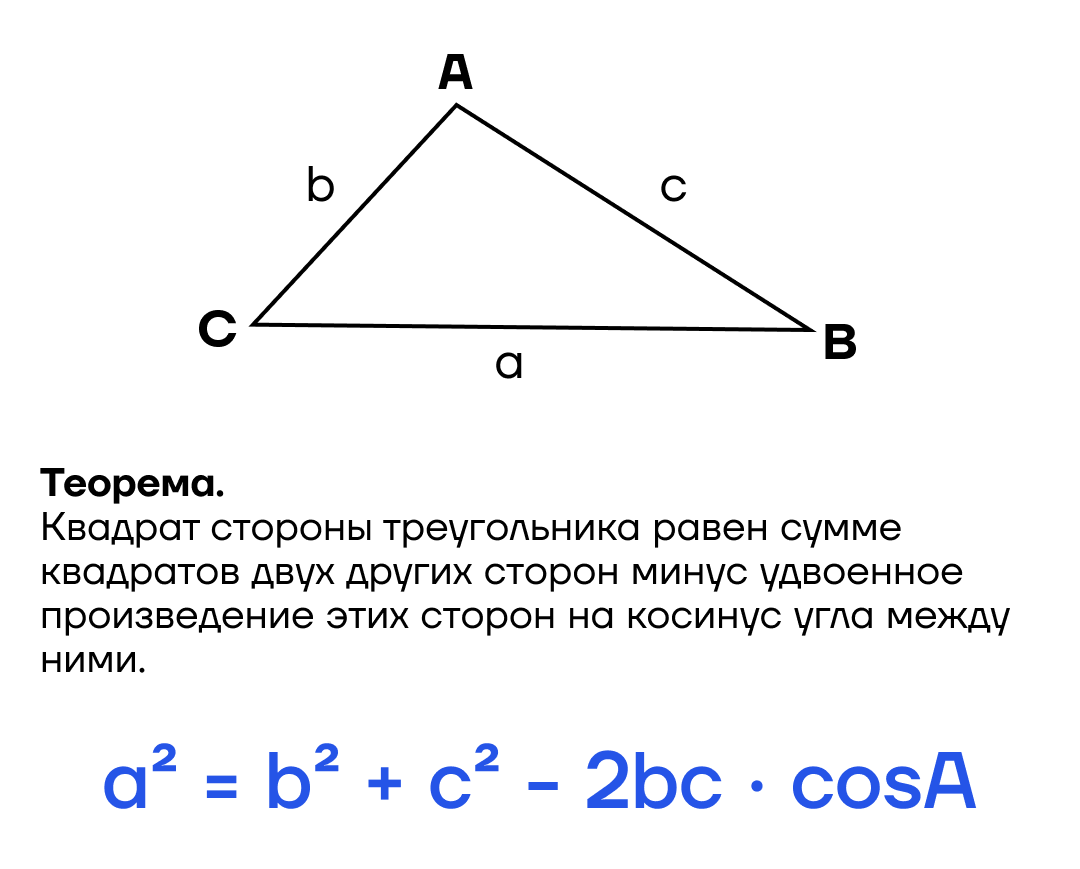
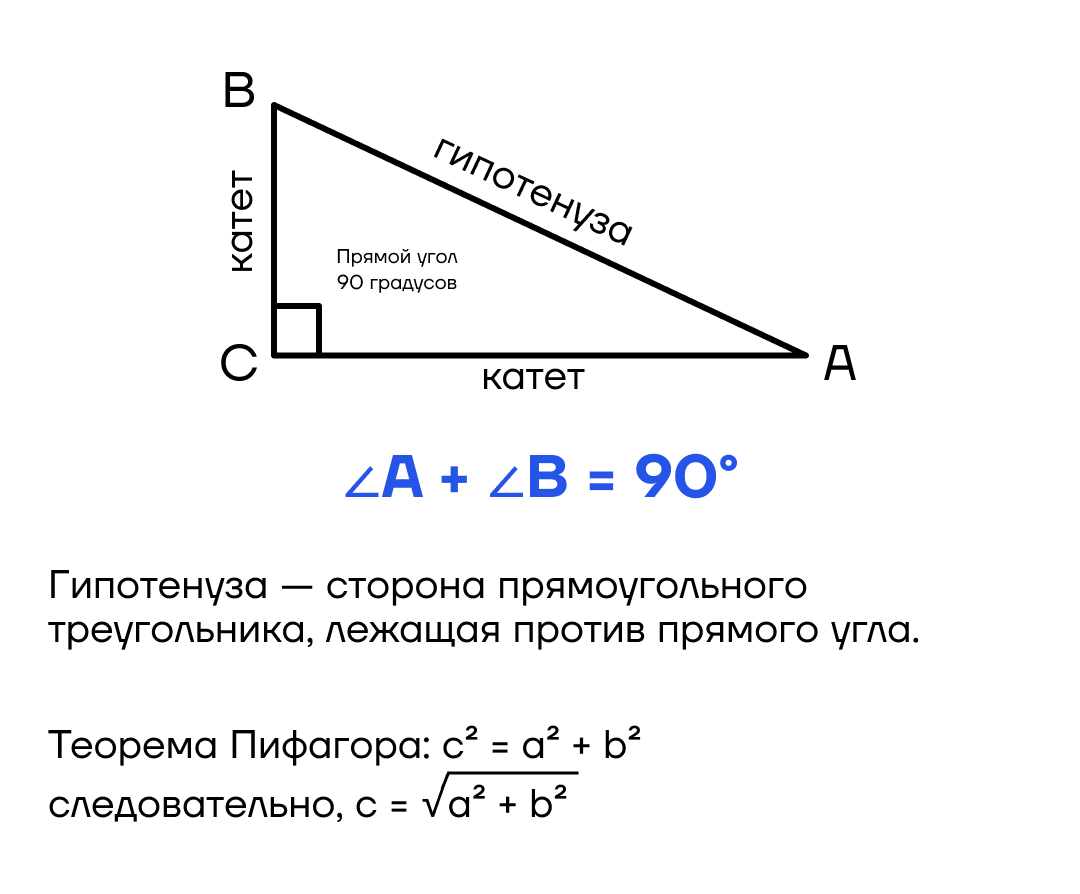
По теореме Пифагора можно найти длину гипотенузы, если известны два катета. Также можно узнать катет, если известна гипотенуза и один из катетов.

Тригонометрические функции в прямоугольном треугольнике

Прямоугольный треугольник с углами 30 и 60 градусов

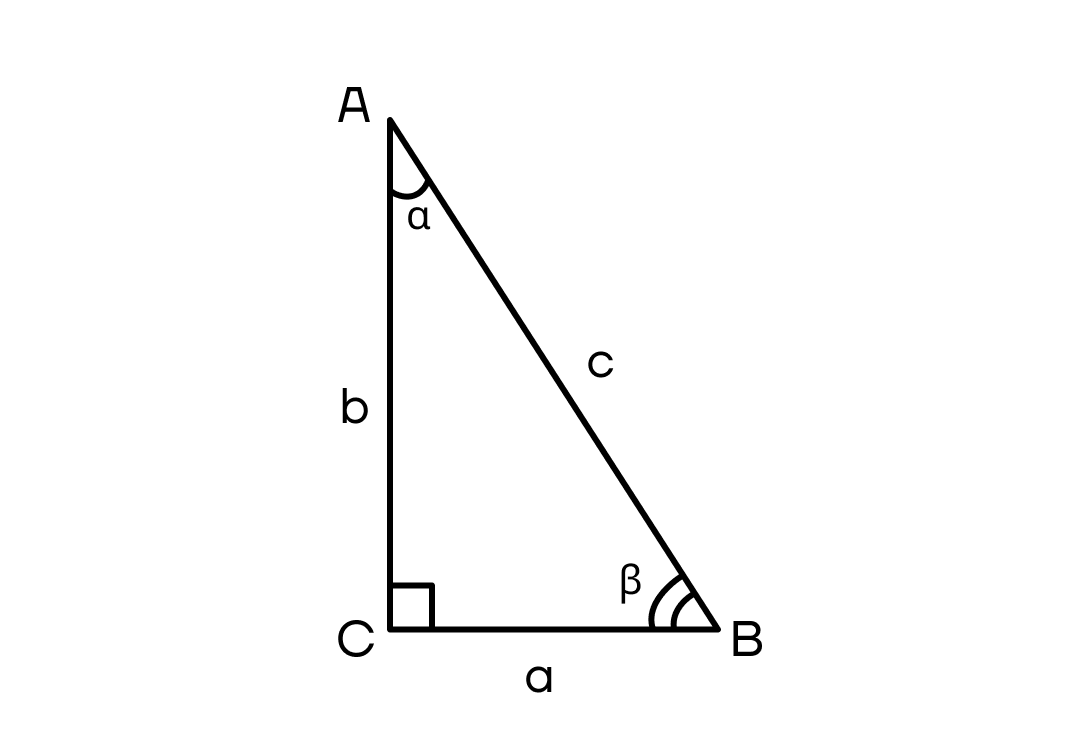
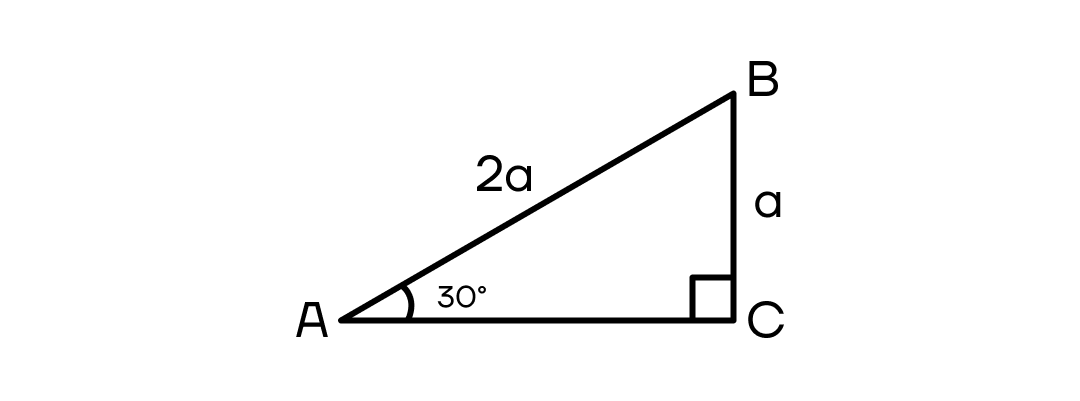
Против угла в 30° лежит катет, равный половине гипотенузы.

Прямоугольный треугольник с углом 45 градусов

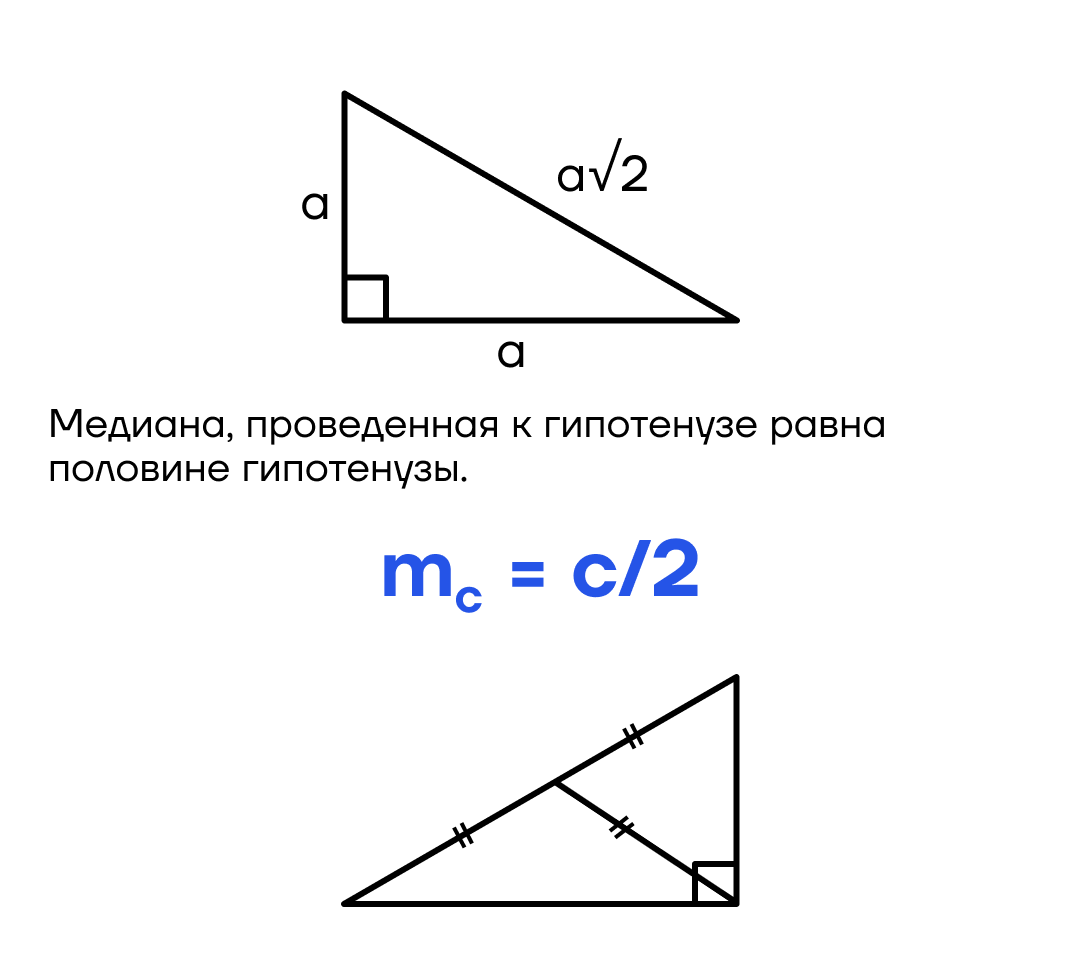
Если один острый угол прямоугольного треугольника равен 45°, то и второй угол прямоугольного треугольника равен 45°.

Следовательно, треугольник будет не только прямоугольным, но и равнобедренным.

3 признака равенства треугольников

1. По двум сторонам и углу между ними.

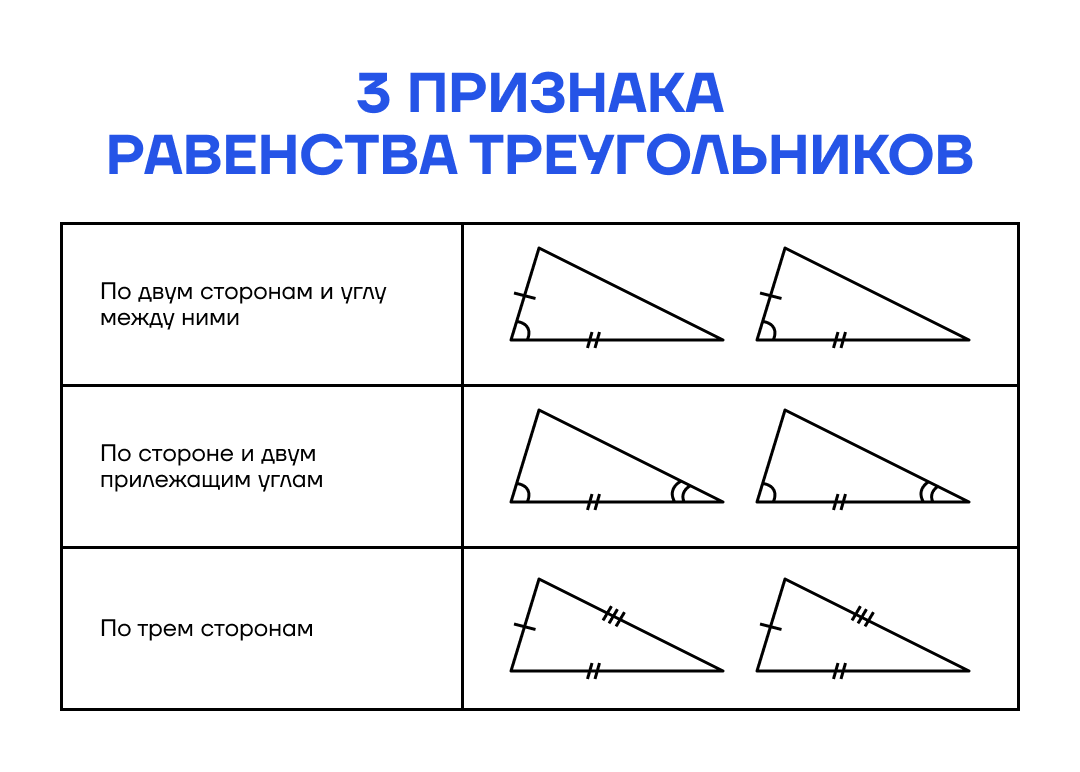
Если две стороны и угол между ними одного треугольника соответственно равны двум сторонам и углу между ними другого треугольника, то такие треугольники равны.

2. По стороне и двум прилежащим к ней углам.

Если сторона и два прилежащих к ней угла одного треугольника соответственно равны стороне и двум прилежащим к ней углам другого треугольника, то такие треугольники равны.

3. По трем сторонам.

Если три стороны одного треугольника соответственно равны трем сторонам другого треугольника, то такие треугольники равны.

3 признака подобия треугольников

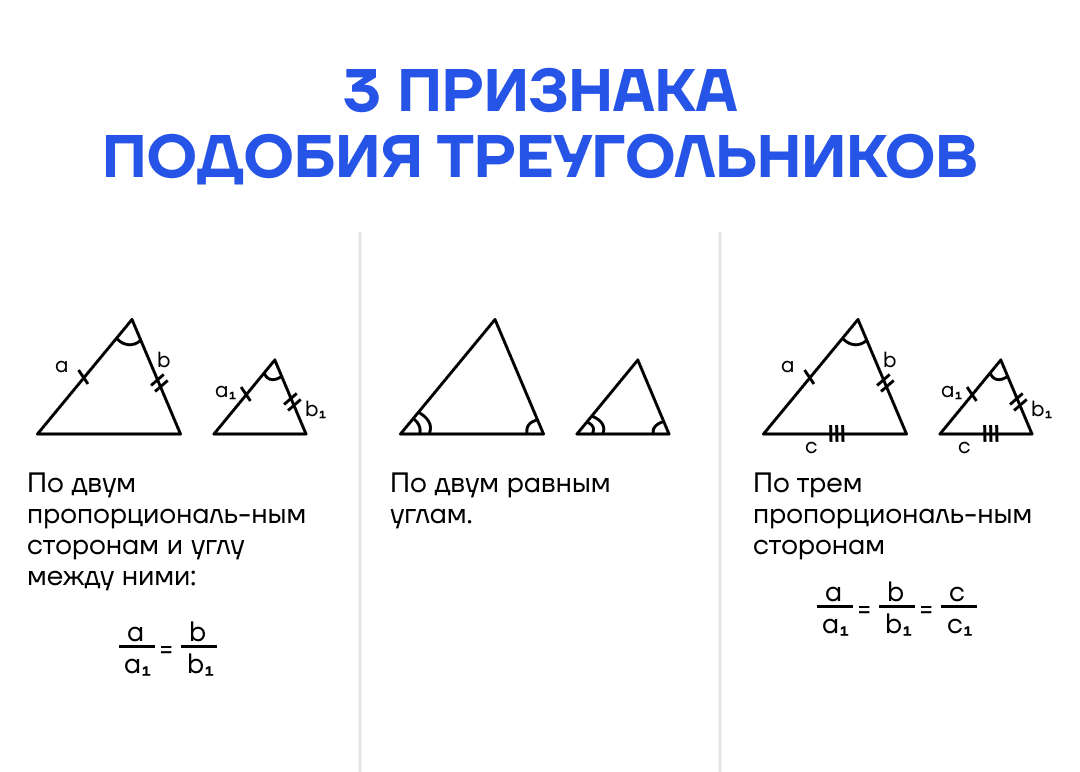
1. По двум пропорциональным сторонам и углу между ними.

Если две стороны одного треугольника пропорциональны двум сторонам другого треугольника, а углы, заключенные между этими сторонами равны, то такие треугольники подобны.

2. По двум углам.

Если два угла одного треугольника равны двум углам другого треугольника, то такие треугольники подобны.

3. По трем пропорциональным сторонам.

Если стороны одного треугольника пропорциональны сторонам другого треугольника, то такие треугольники подобны.

Площади подобных треугольников относятся как коэффициент подобия в квадрате.